NGSolve in Jupyter-Notebook#
Of course, in a Jupyter-Book we can also intregrate Jupyter-Notebooks directly.
import numpy as np
import matplotlib.pyplot as plt
from ngsolve.meshes import MakeStructured2DMesh
from ngsolve import *
from ngsolve.solvers import Newton
from ngsolve.webgui import Draw
#mesh = Mesh(unit_square.GenerateMesh(maxh=0.2))
mesh = MakeStructured2DMesh(quads=False,nx=8,ny=8, mapping = lambda x,y : (x,y))
As example we are looking for solutions to the so-called Gelfands equation:
\[- \Delta u = \lambda e^u \quad \ \text{for}\ x \in \Omega\]
with Dirichlet boundary condition \(u=0\) on \(\partial\Omega\). From the analysis of the equation we know that for \(\Omega \subset \mathbb{R}^2\) there exists a \(0 < \lambda^* < \infty\) such that for \(0 < \lambda < \lambda^*\) we have two solutions. To compute this solutions numerically we use a \(H^1\) FEM discretisation and a path tracking method.
The main idea in pseudoarclength continuation is to drop the natural parametrization by \(\lambda\) and use somit other parametrization [Kel86]. Consider the equation
(7)#\[G(u,\lambda) = 0\]
where \(G: H_0^1(\Omega) \times \mathbb{R} \to \mathbb{R}\). If \((u_0, \lambda_0)\) is any point on a regular path and \((\dot{u}, \dot{\lambda})\) is the unit tangent to the path, then we adjoin to (7) the scalar normalization:
(8)#\[N(u, \lambda, s) = \theta\ \langle\dot{u}_0, (u-u_0)\rangle + (1-\theta)\ \dot{\lambda}_0 \cdot (\lambda - \lambda_0) - (s-s_0) = 0\]
Now we solve (7) and (8) simultaneously for \((u(s), \lambda(s))\). For the implementation with ngsolve we use a product space. For \(u\) a \(H^1\)-FE space and for \(\lambda\) a numberspace:
order = 4
V = H1(mesh, order=order, dirichlet='bottom|right|top|left')
W = NumberSpace(mesh)
X = V*W
# proxy-functions for X
(u,lam) = X.TrialFunction()
(v,q) = X.TestFunction()
# solution
gfx = GridFunction(X)
gfu, gflam = gfx.components
# linearization point
gfx0 = GridFunction(X)
gfu0, gflam0 = gfx0.components
# tangent to the path
dgfx0 = GridFunction(X)
dgfu0, dgflam0 = dgfx0.components
# old tangent to the path
dgfx0_ = GridFunction(X)
dgfu0_, dgflam0_ = dgfx0_.components
AOmega = Integrate(1,mesh)
s0 = Parameter(0)
s = Parameter(0)
theta = Parameter(0.75)
aX = BilinearForm(X)
aX += (grad(u)*grad(v)-lam*exp(u)*v)*dx
aX += (theta*dgfu0*(u-gfu0)*q+(1-theta)*dgflam0*(lam-gflam0)/AOmega*q-(s-s0)/AOmega*q)*dx
We will briefly describe how to compute the tangent vectors \((\dot{u}_0, \dot{\lambda}_0)\). They must satisfy
(9)#\[\begin{split}\begin{split}
G_u^0 \dot{u}_0 + G_\lambda^0 \dot{\lambda}_0 & = 0\\
\theta\ \| \dot{u}_0\|^2 + (1-\theta)\ |\dot{\lambda}_0|^2 & = 1
\end{split}\end{split}\]
For a regular point \(G_u^0\) is nonsingular. We find \(\phi_0\) from the first equation of (9)
\[G_u^0 \phi_0 = -G_\lambda^0 \dot{\lambda}_0\]
Then set
\[\dot{u}_0 = a\,\phi_0\quad\text{and}\quad\dot{\lambda}_0 = a\]
where \(a\) is determined from the second equation of (9)
\[a = \frac{\pm 1}{\sqrt{(1-\theta)+ \theta\,\|\phi_0\|^2}}.\]
In ngsolve we define the linearization as follows
u,v = V.TnT()
dGlam0 = LinearForm(V)
dGlam0 += -exp(gfu0)*v*dx
dGlam = LinearForm(V)
dGlam += -exp(gfu)*v*dx
dGu0 = BilinearForm(V)
dGu0 += (grad(u)*grad(v)-gflam0*exp(gfu0)*u*v)*dx
The initial solution for \(\lambda = 0\) is given by \(u\equiv 0\).
gflam0.Set(0)
gfu0.vec[:] = 0
gfx.vec.data = gfx0.vec
Now we can compute the path
dGlam0.Assemble()
dGu0.Assemble()
dgfu0.vec.data = -dGu0.mat.Inverse(V.FreeDofs())*dGlam0.vec
dgflam0.Set(1/np.sqrt(theta.Get()*Integrate(dgfu0*dgfu0,mesh)+(1-theta.Get())))
dgfu0.vec.data *= dgflam0.vec[0]
dgfx0_.vec.data = dgfx0.vec
lami = [gflam.vec[0]]
mip = mesh(0.5,0.5)
soli = [gfu(mip)]
deltas = 1e-2
N = 90
M = 10
theta.Set(0.75)
scene = Draw(gfu);
gfxsol = GridFunction(X, multidim=N)
for i in range(N):
for j in range(M):
s.Set(s.Get()+deltas)
# solving the coupled system
ret = Newton(aX, gfx, printing=False)
soli.append(gfu(mip))
lami.append(gflam.vec[0])
j += 1
scene.Redraw()
s0.Set(s.Get())
gfx0.vec.data = gfx.vec
dGlam0.Assemble()
dGu0.Assemble()
dgfu0.vec.data = -dGu0.mat.Inverse(V.FreeDofs())*dGlam0.vec
dgflam0.Set(1/np.sqrt(theta.Get()*Integrate(dgfu0*dgfu0,mesh)+(1-theta.Get())))
dgfu0.vec.data *= dgflam0.vec[0]
gfxsol.vecs[i].data = gfx0.vec
sign = Integrate(dgfu0*dgfu0_,mesh)+dgflam0.vec[0]*dgflam0_.vec[0]
if sign < 0:
dgfx0.vec.data *= -1
dgfx0_.vec.data = dgfx0.vec
print(i, '/',N,'dlam0=',dgflam0.vec[0], 'lambda=',gflam.vec[0])
Show code cell output
0 / 90 dlam0= 1.9947016194551224 lambda= 0.19948086777910376
1 / 90 dlam0= 1.9944763203081313 lambda= 0.3989399732713339
2 / 90 dlam0= 1.9942345004901143 lambda= 0.5983757446580947
3 / 90 dlam0= 1.9939743917635706 lambda= 0.7977864445260188
4 / 90 dlam0= 1.9936939723044136 lambda= 0.9971701465060976
5 / 90 dlam0= 1.9933909204137588 lambda= 1.1965247077208414
6 / 90 dlam0= 1.9930625578336616 lambda= 1.3958477361145014
7 / 90 dlam0= 1.9927057798618577 lambda= 1.595136551496392
8 / 90 dlam0= 1.992316968566263 lambda= 1.7943881388056695
9 / 90 dlam0= 1.9918918841745277 lambda= 1.9935990916798147
10 / 90 dlam0= 1.9914255280137918 lambda= 2.19276554383885
11 / 90 dlam0= 1.9909119679901495 lambda= 2.3918830850261408
12 / 90 dlam0= 1.99034411420447 lambda= 2.590946657191516
13 / 90 dlam0= 1.9897134274085657 lambda= 2.789950425140868
14 / 90 dlam0= 1.9890095358433317 lambda= 2.9888876138243
15 / 90 dlam0= 1.9882197253374725 lambda= 3.1877503015111532
16 / 90 dlam0= 1.9873282513864083 lambda= 3.386529153867709
17 / 90 dlam0= 1.9863153969491734 lambda= 3.5852130777177766
18 / 90 dlam0= 1.9851561602325831 lambda= 3.7837887639014363
19 / 90 dlam0= 1.9838183928528674 lambda= 3.9822400742795683
20 / 90 dlam0= 1.9822601025640196 lambda= 4.180547205360942
21 / 90 dlam0= 1.980425452797279 lambda= 4.37868552461928
22 / 90 dlam0= 1.9782386687873557 lambda= 4.576623915055607
23 / 90 dlam0= 1.975594466068399 lambda= 4.774322359524645
24 / 90 dlam0= 1.9723424734377768 lambda= 4.971728310394504
25 / 90 dlam0= 1.9682608042715797 lambda= 5.168771042468545
26 / 90 dlam0= 1.9630089383849172 lambda= 5.365352501993733
27 / 90 dlam0= 1.9560385237757603 lambda= 5.561331727041472
28 / 90 dlam0= 1.946411513644762 lambda= 5.756496660107386
29 / 90 dlam0= 1.9323927375253276 lambda= 5.950509078795476
30 / 90 dlam0= 1.9104167549050939 lambda= 6.1427856659373425
31 / 90 dlam0= 1.8719804307939987 lambda= 6.332203558577294
32 / 90 dlam0= 1.791630391103218 lambda= 6.5162115102567615
33 / 90 dlam0= 1.557686378724325 lambda= 6.687150285508426
34 / 90 dlam0= 0.33825054754330414 lambda= 6.805451140159947
35 / 90 dlam0= -1.3231832883709755 lambda= 6.722737474319122
36 / 90 dlam0= -1.6217451546066024 lambda= 6.571000296425428
37 / 90 dlam0= -1.7304228300468476 lambda= 6.402349081121052
38 / 90 dlam0= -1.7847989447795383 lambda= 6.226213813222953
39 / 90 dlam0= -1.8168393897381365 lambda= 6.045960620964525
40 / 90 dlam0= -1.8376044569548577 lambda= 5.863147114143483
41 / 90 dlam0= -1.8518763729262901 lambda= 5.678619006149821
42 / 90 dlam0= -1.8620444081179512 lambda= 5.492888359433755
43 / 90 dlam0= -1.8694283526932056 lambda= 5.30629114660011
44 / 90 dlam0= -1.8748120240213377 lambda= 5.119062189838897
45 / 90 dlam0= -1.8786861494181095 lambda= 4.931374504465813
46 / 90 dlam0= -1.8813695644036552 lambda= 4.743361617219981
47 / 90 dlam0= -1.8830741294808606 lambda= 4.555131061746294
48 / 90 dlam0= -1.8839414535196664 lambda= 4.366773008441202
49 / 90 dlam0= -1.8840645180045799 lambda= 4.178366081038669
50 / 90 dlam0= -1.8835007193187339 lambda= 3.9899814928719572
51 / 90 dlam0= -1.8822797414344452 lambda= 3.801686165472514
52 / 90 dlam0= -1.8804081072687193 lambda= 3.613545241101018
53 / 90 dlam0= -1.8778714168838841 lambda= 3.4256242637051044
54 / 90 dlam0= -1.8746347941403771 lambda= 3.2379912290915938
55 / 90 dlam0= -1.8706417496001373 lambda= 3.0507186699072917
56 / 90 dlam0= -1.8658114293670338 lambda= 2.8638859325404735
57 / 90 dlam0= -1.860033995773557 lambda= 2.6775818170110592
58 / 90 dlam0= -1.853163625628271 lambda= 2.4919077884021714
59 / 90 dlam0= -1.8450082573702316 lambda= 2.3069820356961928
60 / 90 dlam0= -1.8353146860074518 lambda= 2.1229447640957577
61 / 90 dlam0= -1.823746754093804 lambda= 1.9399652837905998
62 / 90 dlam0= -1.809852965291463 lambda= 1.75825174405836
63 / 90 dlam0= -1.793017369700893 lambda= 1.578064833683035
64 / 90 dlam0= -1.7723830530191245 lambda= 1.3997375727628107
65 / 90 dlam0= -1.7467288730373332 lambda= 1.2237047475868452
66 / 90 dlam0= -1.7142622743264078 lambda= 1.050548206872232
67 / 90 dlam0= -1.672251786282651 lambda= 0.8810695557151766
68 / 90 dlam0= -1.6163306547533143 lambda= 0.7164132010973521
69 / 90 dlam0= -1.5390840219738866 lambda= 0.5582888010044538
70 / 90 dlam0= -1.427113960571574 lambda= 0.40940075625557565
71 / 90 dlam0= -1.2560440761359621 lambda= 0.2742780649977424
72 / 90 dlam0= -0.9922912258123794 lambda= 0.16044997793245902
73 / 90 dlam0= -0.6295534406052508 lambda= 0.07699770265807715
74 / 90 dlam0= -0.2868749677519353 lambda= 0.030690486471914698
75 / 90 dlam0= -0.10409381179788102 lambda= 0.01261184222254576
76 / 90 dlam0= -0.043002248250081344 lambda= 0.005766256381688732
77 / 90 dlam0= -0.019661140162135826 lambda= 0.002801503373359672
78 / 90 dlam0= -0.009525474279522573 lambda= 0.0014078651143380255
79 / 90 dlam0= -0.0047836978081387095 lambda= 0.0007209586206671448
80 / 90 dlam0= -0.002474140055883422 lambda= 0.00037031111336795615
81 / 90 dlam0= -0.0013306261703183461 lambda= 0.00018553825891673507
82 / 90 dlam0= -0.0006607043206693135 lambda= 8.938085500352027e-05
83 / 90 dlam0= -0.000317057333611176 lambda= 4.254322087058004e-05
84 / 90 dlam0= -0.0001506532801845776 lambda= 2.0185721635393847e-05
85 / 90 dlam0= -7.138481744270805e-05 lambda= 9.578320199215052e-06
86 / 90 dlam0= -3.383075485258497e-05 lambda= 4.5522580839556405e-06
87 / 90 dlam0= -1.6060058324831122e-05 lambda= 2.1686105547322314e-06
88 / 90 dlam0= -7.64257672944812e-06 lambda= 1.0358313898363442e-06
89 / 90 dlam0= -3.646930995584269e-06 lambda= 4.961037050977722e-07
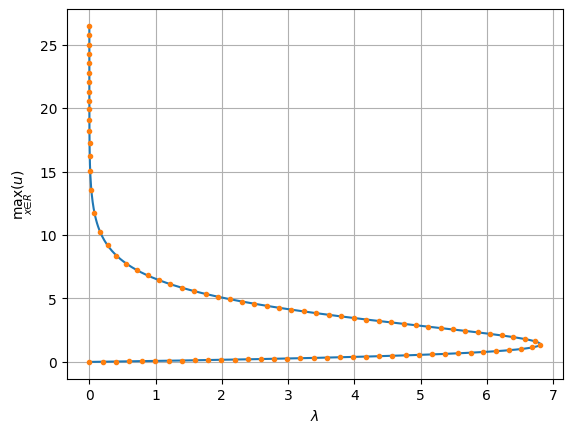
plt.plot(lami,soli,'-')
plt.plot(lami[::M],soli[::M],'.')
plt.grid()
plt.xlabel('$\lambda$')
plt.ylabel('$\max_{x\in R}(u)$')
plt.show()
Draw(gfxsol.components[0],mesh,min=0,max=8,interpolate_multidim=True,
autoscale=False, animate=True, settings = { "subdivision" : 5, "Colormap" : { "ncolors" : 32 }});